A Reinforcement Learning agent learns to Prepare Quantum States in a non-integrable Ising chain. With no prior knowledge about the quantum system, the agent learns to extract the essential features of the optimal preparation protocol.
Machine Learning (ML) ideas have recently been applied to physics to detect phase transitions [1], and compress quantum mechanical wavefunctions [2]. I have recently become interested in developing and applying Reinforcement Learning (RL) algorithms to study quantum dynamics. RL is a subfield of ML where a computer agent is taught to master a specific task by performing a series of actions in order to maximize a reward function, as a result if interaction with its environment. RL was used in the 90’s to create a computer agent to beat the world’s best backgammon players [3]. Recently, Google DeepMind succeeded in teaching a RL agent to play the video games Atari and Go [4,5]. Inspired by this success, we decided to investigate what insights in physics can be gained from such an approach.
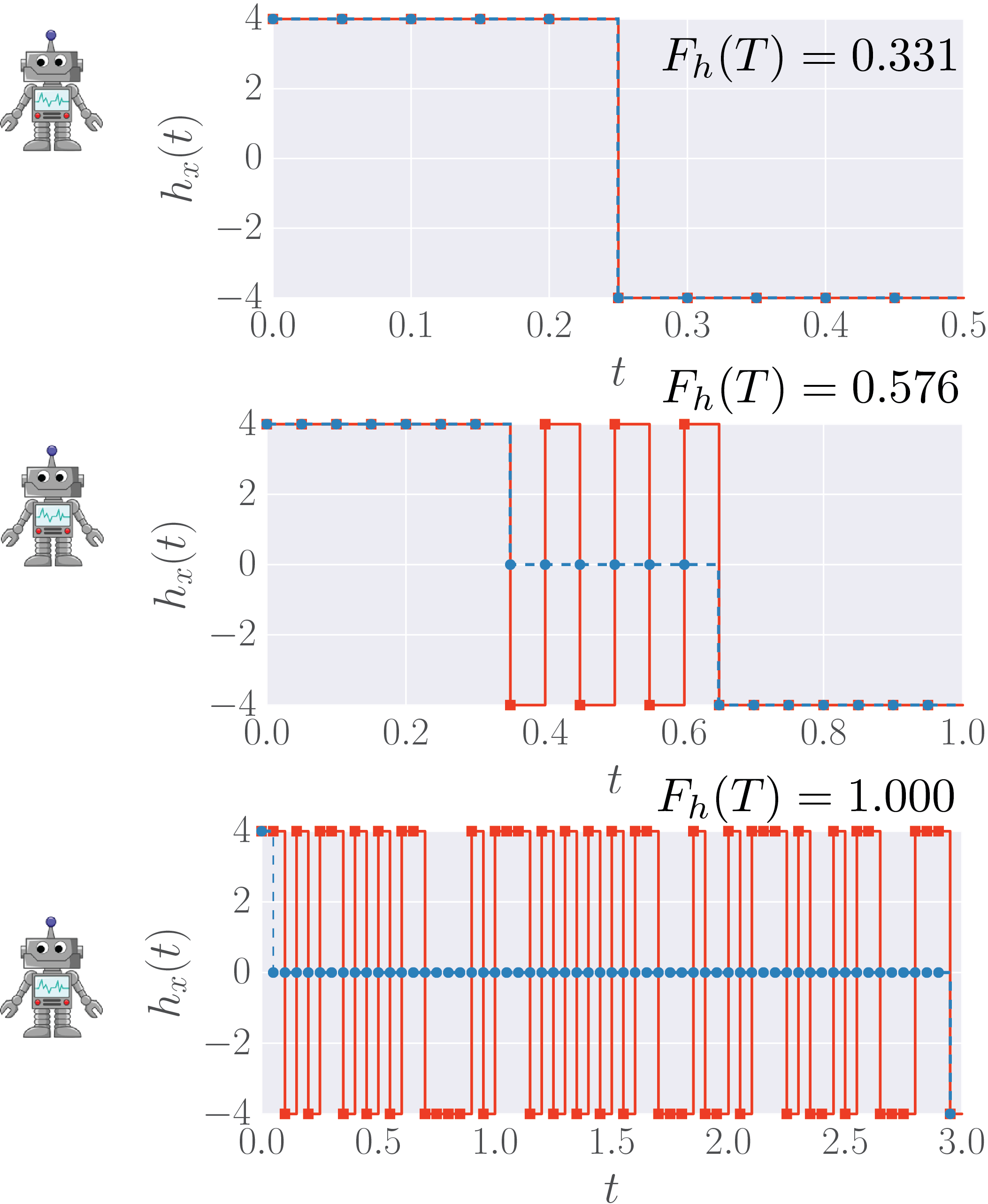
How does it Work?—We used a modified version of Watkins online Q-learning algorithm with linear function approximation and eligibility traces [6] to teach a RL agent to find an optimal protocol sequence to prepare a quantum system in a pre-defined target state [7]. To manipulate the system, our computer agent constructs piecewise-constant protocols of duration $T$ by choosing a drive protocol strength $h_x(t)$ at each discrete time step $t$. One can think of $h_x(t)$ as a magnetic field applied to the system or, more generally — as a control knob. In order to make the agent learn, it is given a reward for every protocol it constructs – the fidelity $ F_h(T)=\lvert \langle\psi_\ast \vert \psi(T)\rangle
\rvert ^2 $ for being in the target state after time $T$ following the protocol $h_x(t)$ obeying the laws of Quantum Dynamics. The goal of the agent is to maximize the reward $ F_h(T)$ in a series of attempts. Deprived of any knowledge about the underlying physical model, the agent collects information about already tried protocols, based on which it constructs new, improved protocols through a sophisticated biased sampling algorithm[RL paper]. For simplicity, consider bang-bang protocols, (see Fig.), where $h_x(t)\in\{\pm 4\}$, although we verified that RL also works for quasi-continuous protocols with many different protocol steps. You can learn more about our work in this paper.
 |
Model—To test the agent, we decided to prepare states in the transverse-field Ising chain:
\[H(t) = -\sum_{j=1}^L \left( JS^z_{j+1}S^z_j + S^z_j + h_x(t)S^x_j\right)\]To make the model untractable by perturbative analytical calculations, we add a parallel field and choose all couplings to be of the same order of magnitude so there is no small paramter. This model is known to be nonintegrable, and features thermalising (chaotic) dynamics. We choose the paramagnetic ground states of the above Hamiltonian at fields $h_x/J=-2$ and $h_x/J=2$ for the initial and target state, respectively. Even though there is only one control field in the problem, the space of available protocols grows exponentially with the inverse time step size and we have demonstrated numerically that it is exponentially hard to find the optimal protocol [8].
Constrained Qubit Manipulation—To benchmark the performace of the RL agent, let us first set $J=0$, so that the model decouples into a sequence of independent quantum bits, known as qubits. The movie above below shows the learning process of the RL agent for a single qubit. Notice that the protocol the agent finds after a series of attempts has a remarkable feature: without any prior knowledge about the intermediate quantum state nor its Bloch sphere representation [an effective geometric description for the quantum degrees of freedom of a single qubit], the RL agent discovers that it is advantageous to first bring the state to the equator – which is a geodesic – and then effectively turns off the field $h_x(t)$, to enable the fastest possible precession about the $\hat z$-axis. After staying on the equator for as long as optimal, the agent rotates as fast as it can to bring the state as close as possible to the target, thus optimizing the final fidelity for the available protocol duration.
Many Coupled Qubits—Back to the non-integrable model $J=1$, it is impossible to visualise the driving protocol due to the exponentially many degrees of freedom in the problem. However, by putting the system on a closed chain and making use of translation invariance, all qubits behave in the same way on every lattice site. Hence, we can trace out all sites but one, and study the properties of the underlying reduced density matrix of the remaining qubit on the Bloch sphere. The second movie shows how our RL agent learns the physics of the many-body system. This counter-intuitive solution can also be found using optimal control algorithms, such as GRAPE [9], and hints towards the existence of bizzare principles that govern the physics of systems away from equilibrium.
References:
[1] J. Carrasquilla and R. G. Melko, Nat. Phys. 13, 431 (2017).
[2] G. Carleo and M. Troyer, Science 355, 602 (2017).
[3] G. Tesauro, Communications of the ACM. 38 (3) (1995).
[4] V. Mnih et al., Nature 518, 529 (2015), letter.
[5] D. Silver,et al., Nature 529, 484 (2016), article.
[6] R. S. Sutton and A. G. Barto, Reinforcement Learning: An Introduction (MIT Press, Cambridge, MA, 2017).
[7] M.B., A. G.R. Day, D. Sels, P. Weinberg, A. Polkovnikov, and P. Mehta, Phys. Rev. X 8 031086 (2018).
[8] A. G.R. Day, M.B., P. Weinberg, P. Mehta, and D. Sels, arXiv: 1803.10856 (2018).
[9] N. Khaneja, T. Reiss, C. Kehlet, T. Schulte-Herbrüggen, and S. J. Glaser, Journal of Magnetic Resonance 172, 296 (2005).
Copyright © 2017 Marin Bukov